Geometric Deep Learning on Protein Design
MEng Material Science and Engineering Master Thesis
Supervisor: Prof. Stefano Angioletti-Uberti | Theory and Simulation of Materials
Graph Neural Network | Group Representation Theory | Rotation Invariant | Spherical Harmonics
In the world of biomolecular prediction, it's easy to get caught up in the latest techniques like multiple heads of pairwise attention and overparameterized MLP sub-layers. But are these methods the best way to go about it? One promising direction is the use of Graph Neural Networks and Group Representation Theory. These methods explicitly incorporate the unique structure and properties of biomolecules, and can lead to more precise and lightweight models with stronger inductive bias. For example, by utilizing features like Rotation Invariant Spherical Harmonics, these models can achieve greater accuracy while using fewer parameters. Gone are the days of relying solely on scaled-up models in the hopes of achieving better predictions. Instead, we must strive for efficiency in biomolecular representation. By embracing novel techniques and approaches, we can unlock the full potential of biomolecular prediction and make significant strides in our understanding of the intricacies of nature.
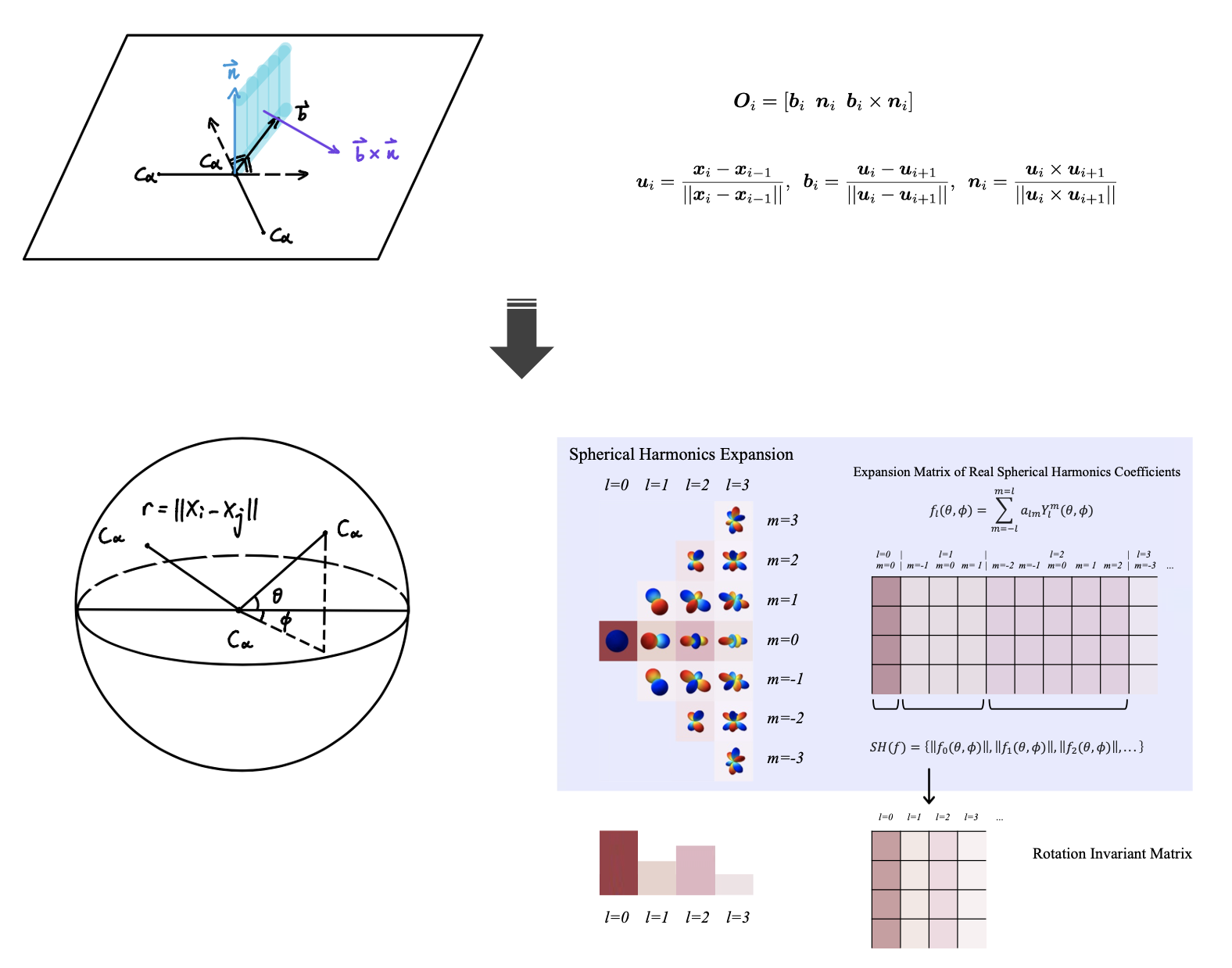
Protein design, the creation or modification of proteins with specific functions or properties through laboratory experiments or computational methods, is a major challenge in molecular biology and biochemistry. The ability to "custom-build" proteins has the potential to generate new drugs, enzymes, and other biomolecules with useful functions in biotechnology and medicine. To achieve this, it is necessary to understand how the three-dimensional structure and function of a protein are encoded in its amino acid sequence.
Data-driven approaches have recently opened up new opportunities for protein design by enabling the learning of sequence-structure relationships. This presents a promising avenue for making progress in the setting of multi-body interactions where traditional methods based on first principles may be limited. Current efforts in this field are focused on designing new biological functions and their applications, with most research centered on structural representations. A major challenge in protein structural representations is the lack of robustness to the rotational degrees of freedom of protein.
To address this issue, we present an approach for constructing rotation-invariant representations for the inverse protein folding problem using spherical harmonics. Spherical harmonics are a set of functions defined on the surface of a sphere. These functions can be combined to form a representation of a protein structure that effectively describes its symmetry, which is invariant to rotations and has lower dimensions, enabling a faster training process and prediction of amino acid sequences from a more efficient 3D structural description.We evaluated the proposed approach using ProteinMPNN and compared it to a number of benchmark molecular descriptors to demonstrate its effectiveness in protein design.